Lacock Abbey,
Dec. 19. 1834

My Dear Sir

I am aware that the integral I have considered, 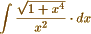may be transformed into 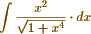. But I expect from Abel's Theorem ^<1> a solution of the problem without the help of a previous transformation. For my method requires none, but gives the required solution at once, by means of a commodious notation which I have devised for that purpose. - I should be glad to see the solution of 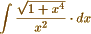according to Abel's theorem, written out at length and no step omitted, as I cannot make it out, owing no doubt to my want of familiarity with his manner of viewing the subject. - I have to return my thanks for your offer of sending me Legendre ^<2> &c from the library of the R. Society. ^<3> But I posses his works complete, as well as Crelle's Annals, ^<4> a work of great value, too little known in this country.

I have begun to examine Abel's Theorem with attention. It appears to me applicable to all integrals of the form 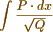where P and Q are rational functions of x. But tho' applicable, I doubt whether the length of the calculations will not frequently prevent the true result from being obtained - But it does not seem applicable to the integral 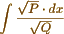much less to the form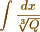 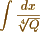  &c. &c. which my method resolves in innumerable instances as I hope to show. Will you have the goodness to examine whether the following integral viz. 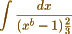is capable of integration by Abel's theorem, or in any other way hitherto known? I have not examined into what other forms it may be transformed, but have obtained a [illegible deletion] direct solution, which I am endeavoring to put to the test of arithmetical verification to the extent of six places of decimals - But these calculations are very prolix.

n being any whole number, my method gives the solution at once, but not a real solution, except in particular instances. The imaginary quantities which enter into the result do not however prevent it from being analytically true, as appears from Legendre's calculation of the sum of 2 imaginary integrals in his last supplement; and as indeed might be concluded with certainty, even without such proof.

With regard to the constant of integration, if you will consider the subject with respect to the integral 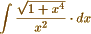(which is my example) you will see I think that it depends entirely upon the value of x which you assume for the commencement of the integration, and that as this value is entirely arbitrary, so also is the constant capable of an infinite variety of values. These are always algebraic, and not transcendents except when the initial value of x is so, which we do not suppose. - I have examined why Legendre finds transcendent constants in his supplement, and I think I see clearly the reason of that.

I have not heard from Peacock ^<5> lately, I am afraid he is ill, as he told me in his last that he had been so - I find on looking thro' my papers on the Integral Calculus that they are so many that it will take me some time to put them in order. - You give me in your letter the solution of the equation

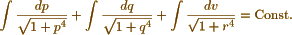
But now let me ask you to examine what solution Abel's theorem gives when there are only 2 quantities, viz.

If you please I will send you the solution of the latter problem which I consider rather a difficult example in my next letter. I mean, if the 2 following particular integrals are excluded, viz. p + q = 0 and pq = 1

No doubt, as you say, these may be transformed into elliptic integrals. I know not what result would be obtained, but the calculations would probably be much longer than necessary.

Believe me to remain Yours very truly
H.F. Talbot

P.S. You have directed your letter to "the Hon^ble &c." which is a title I have no claim to. Would the R. Society admit into their Transactions a paper of great length on this subject in short a full exposition of the methods of integration which I do not profess to find the complete algebraic integral of the equations I examine, nor does Abel, in fact its complexity, if found, would seldom permit it to be of any use.

1834 Chippenham December twenty H.F. Talbot
J.W. Lubbock Esq.
29 Eaton Place
Mildred Court
London

---

Notes:

1. Written in 1824, lost in Paris and re-written in 1828, this theorem proved the impossibility of solving equations of the fifth degree (quintic equations) through the use of radicals.

2. Adrien Marie Legendre (1752-1833), mathematician. [See Doc. No: 03014].

3. The Royal Society, London.

4. August Leopold Crelle (1780-1855), German mathematician, Journal Für Die Reine Und Angewandte Mathematik, first printed in 1826. [See Doc. No: 03046].

5. Prof George Peacock (1791-1858), mathematician.