Lacock Abbey,
27^th Jan^ry 1835

Dear Sir,

I have looked at Abel’s letter to Legendre in Crelle’s Annals vol 6. p.78 ^<1> – In this place he appears to me to announce an important theorem respecting integrals of the form where the radical m is any number whatever. He says “Rien n’est plus facile que le démonstration de ce théorême. Je le donnerai dans un de mes mémoires prochains.” ^<2> But it does not appear that he lived to publish this demonstration & therefore it may long remain as a sort of enigma for mathematicians to try their skill at, like Fermat’s celebrated theorems ^<3> some of which remain undemonstrated to the present day – Although he says “Rien n’est plus facile” yet without some further clue to the method he pursued in discovering it, it may not be easy to make out the demonstration.

I wish he had given one or two easy examples of the application of this new theorem to the simplest case after the quadratic radicals, namely to the 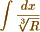we should then have seen his meaning more clearly.

I have referred at your desire ^<4> to what Legendre says of the integrals (vol.2. p.382) ^<5>

But since he calls this integral and treats it as a particular case of which is, according to the definition in page 366 the value of a certain integral between the limits 0 and 1, it follows that his demonstration in p. 382 has the same limitation, and therefore nothing can be concluded from it with regard to the general properties of the integral.

You observe that my integral 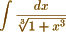is reducible to the form . How does that appear? and that it may be reduced to an elliptic, according to Legendre; but you do not quote the vol. & page otherwise I should be glad to refer to what he says.– Perhaps you will have the goodness to supply this omission.

Believe me to remain Yours vy truly
H. F. Talbot

P.S. I am not in the present parliament, having retired to avoid the expense of a contested election. I have calculated an arithmetical example of the application of my method to a cubic radical. The result came out correct in the five first decimals.

J.W. Lubbock Esq^re
29 Eaton Place
London

---

Notes:

1. Niels Henrik Abel (1802–1829), mathematician to Adrien Marie Legendre, ‘Fernere mathematische Bruchstücke aus Herrn N. H. Abel’s Briefen’, Journal Für Die Reine Und Angewandte Mathematik, v. 6 no. 1, item 6, 1830, pp. 73–80.

2. Nothing is easier than the demonstration of this theorem. I will give it in my next paper.

3. Pierre de Fermat (1601–1665) stated in his famous last theorem that, xn + yn = zn has no non-zero integer solutions for x, y and z when n > 2, and promised a proof of this, but none was ever found among his papers.

4. Letter not located.

5. Adrien Marie Legendre, Traité des fonctions elliptiques et des intégrals eulériennes avec des tables pour en faciliter le calcul numérique (Paris: Huzard-Courcier) 1825. Supplements printed 1828.