Gènes
le 27 Octobr 1822
Monsieur
Je viens de recevoir dans cet instant la reponse de M. Spooner, <1> et crainte que cette lettre ne vous trouve plus à Florence, je m’empresse de vous l’envoyer en toute hâte, voici ce qu’il me marque
“The equation (pag. 333 Corresp.) <2> is not correctly printed, but the error does not affect the conclusion your Correspondent obtains. That equation is there printed.
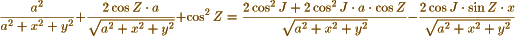
It ought to have been printed
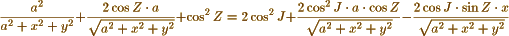
The same equation is again wrong printed in the enunciation of Proposition the 4th (cahr I) The last member of that equation is there printed 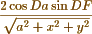 but ought to have been printed
but ought to have been printed

In the corollary also to that proposition the equation reduced to a better form is once printed  If then (as your correspondent proposes) we make A infinite with respect to X and Y we obtain
If then (as your correspondent proposes) we make A infinite with respect to X and Y we obtain
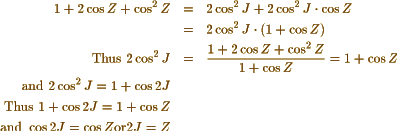
Now this conclusion is entirely correct, for by taking A infinite with respect to X and Y, we limit the luminous area to the spot immediately below the Eye of the spectator, and it appears from the observations that follow the corollary to the 2d. Proposition, that when a Ray of light is reflected to the spectator from the spot immediately below that where his Eye is placed that the double of the angle which measures the inclination of that plane by which that Ray has been so reflected will equal the Sun’s zenith distance at that moment.
As by taking A infinite with respect to X and Y you thus obtain, the equation between the Sun’s zenith distances and the greatest inclination of the Wave when the luminous appearance extends exactly to the spot where the spectator is situated so also by taking X infinite with respect to A and Y, you obtain the equation between the Sun’s zenith distance s and the greatest inclination of the Wave at the moment, when the luminous appearance first touches the horizon (see Propos. 2) Z + 2J = 90 By taking X infinite we obtain
Cos2 z = 2 Cos2 J − 2 Cos2 J Sin. Z
= 2 Cos2 J (1−Sin. Z)
or 1−Sin2 Z = 2 Cos2 J (1−Sin. Z)
or (1−Sin. Z) (1 + Sin. Z) = 2 Cos2 J. (1−Sin. Z.)
or 1 + Sin Z = 2 Cos2 J
= 1 + Cos 2J
Thus, Sin Z = Cos 2J. and Z + 2J = 90
I have observed also with your Correspondent, that when the Phenomenon in question is observed from a great height, the curve is better defined, and account for it, as he does. The distance of the Waves from each other, and their magnitude then becomes infinitely small with respect to the elevation of the Eye of the spectator, and the surface of the sea becomes very nearby indeed such a horizontal plane as I have imagined. on account however of the great distance of the horizon the extent of the luminous arc of the horizon is then left distinctly marked, and it is therefore that I have recommended (pag 332) the observations with a view to deciding the greatest inclination of the reflecting surface of the Waves, to be made at a small elevation above the level of the sea. One circumstance however very remarkable occurs, when this Phenomenon is observed from a considerable elevation.
The horizontal plane formed by the Ridge on the tops of the Waves (p. 337) then extends much farther from the horizon, and consequently a disturbed image of the Sun may be seen for about half an hour before Sun Set in the midelle of the luminous area. I have seen this very distinctly from <illegible deletion> the top of the Lighthouse at Leghorn. &c…
M. Spooner, qui est à Nice, comme j’eus l’honneur de vous le dire, veut que je mette sa reponse dans ma Corresp. mais je ne le ferai, que lorsque vous m’aurez donné la permission de publier votre lettre; dans la quelle vous faites votre objection. Peut-etre aussi, quand vous aurez lu la reponse de M. Spooner, vous arrangerez diffèremment votre question, mais en tout cas, je ne publierai rien, sans avoir reçu votre avis. J’attends par consèquent votre reponse; Si vous etes sur votre départ, vous aurez la bonté de me répondre de Rome. Je finis cette lettre dans la plus grande hâte, parceque le Courier part dans le moment je n’ai plus que le tems de vous assurer de la haute éstime avec la quelle je ne cesse d’être –
Votre très Humble Serviteur
Zach
P.S. Le livre de ce cèlèbre géometre anglais, que vous avez eu la bonté de m’envoyer de Livourne, n’est pas arrivé encore, je serais bien faché s’il était perdu.To Honorble Mr W. H. Talbot.
Poste restante
Florence
Translation:
Genoa
27 October 1822
Sir
I have just this instant received Mr Spooner’s reply, and fearing that this letter will no longer find you in Florence, I hasten to send it to you as quickly as possible. This is what he has marked for me
“The equation (pag. 333 Corresp.) is not correctly printed, but the error does not affect the conclusion your Correspondent obtains. That equation is there printed.
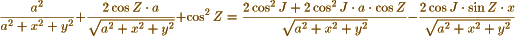
It ought to have been printed
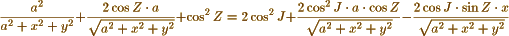
The same equation is again wrong printed in the enunciation of Proposition the 4th (cahr I) The last member of that equation is there printed 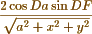 but ought to have been printed
but ought to have been printed

In the corollary also to that proposition the equation reduced to a better form is once printed  If then (as your correspondent proposes) we make A infinite with respect to X and Y we obtain
If then (as your correspondent proposes) we make A infinite with respect to X and Y we obtain
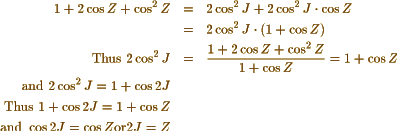
Now this conclusion is entirely correct, for by taking A infinite with respect to X and Y, we limit the luminous area to the spot immediately below the Eye of the spectator, and it appears from the observations that follow the corollary to the 2d. Proposition, that when a Ray of light is reflected to the spectator from the spot immediately below that where his Eye is placed that the double of the angle which measures the inclination of that plane by which that Ray has been so reflected will equal the Sun’s zenith distance at that moment.
As by taking A infinite with respect to X and Y you thus obtain, the equation between the Sun’s zenith distances and the greatest inclination of the Wave when the luminous appearance extends exactly to the spot where the spectator is situated so also by taking X infinite with respect to A and Y, you obtain the equation between the Sun’s zenith distance s and the greatest inclination of the Wave at the moment, when the luminous appearance first touches the horizon (see Propos. 2) Z + 2J = 90 By taking X infinite we obtain
Cos2 z = 2 Cos2 J − 2 Cos2 J Sin. Z
= 2 Cos2 J (1−Sin. Z)
or 1−Sin2 Z = 2 Cos2 J (1−Sin. Z)
or (1−Sin. Z) (1 + Sin. Z) = 2 Cos2 J. (1−Sin. Z.)
or 1 + Sin Z = 2 Cos2 J
= 1 + Cos 2J
Thus, Sin Z = Cos 2J. and Z + 2J = 90
I have observed also with your Correspondent, that when the Phenomenon in question is observed from a great height, the curve is better defined, and account for it, as he does. The distance of the Waves from each other, and their magnitude then becomes infinitely small with respect to the elevation of the Eye of the spectator, and the surface of the sea becomes very nearby indeed such a horizontal plane as I have imagined. on account however of the great distance of the horizon the extent of the luminous arc of the horizon is then left distinctly marked, and it is therefore that I have recommended (pag 332) the observations with a view to deciding the greatest inclination of the reflecting surface of the Waves, to be made at a small elevation above the level of the sea. One circumstance however very remarkable occurs, when this Phenomenon is observed from a considerable elevation.
The horizontal plane formed by the Ridge on the tops of the Waves (p. 337) then extends much farther from the horizon, and consequently a disturbed image of the Sun may be seen for about half an hour before Sun Set in the midelle of the luminous area. I have seen this very distinctly from <illegible deletion> the top of the Lighthouse at Leghorn. &c…
Mr Spooner, who is in Nice, as I had the honour to tell you, wants me to put his reply in my Correspondance, but I will only do so when you have given me permission to publish your letter; in which you give your objection. It is also possible that when you have read Mr Spooner’s reply, you will put your question in a different way, but in any case, I will not publish anything unless I have your opinion. Consequently, I am awaiting your reply from Rome. I am finishing this letter in the greatest haste because the Post will be leaving in a momen, and I only have time to assure you of the high regard with which I continue to be –
Your very Humble Servant
Zach
P.S. The book by that famous English geometrician, which you were kind enough to send me from Leghorn, has not yet arrived, I would be very sorry if it were lost.To Honourable Mr W. H. Talbot.
Poste restante
Florence
Notes:
1. A son of the Isaac Spooner family of Elmdon Hall, Warwickshire.
2. Correspondance astronomique, géographique, hydrographique et statistique du Baron de Zach (Genoa: 1818–1826).


