Montpellier,
le 1r Novembre 1822.
Monsieur,
Vous recevrez peu après cette lettre mon no d’Octobre où vous trouverez plusieurs démonstrations de votre élégant théorème sur les cercles qui touchent les trois côtés d’un même triangle.
Je viens, d’après vos indications, de faire une petite note pour rectifier l’énoncé du problème traité par M. Sagani Michel (pag. 115) et donner la véritable solution. Son équation
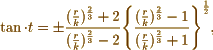
est bien l’équation de votre courbe, dans la quelle k est le demi-diamètre de l’hyperbole, ou ce que vous avez pris pour unité. Mais je n’ai pas bien su comment cette équation se réduisait à la forme très simple
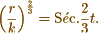
Je crois me rappeler, Monsieur, de vous avoir entendu dire que vous aviez une méthode particuliere, pour la recherche des courbes enveloppes. Il faut que cette méthode soit bien supérieure pour donner de tels résultats. Elle serait très précieuse à connaître; car bien que le problème des enveloppes soit très simple en théorie, on rencontre dans les applications des éliminations de nature à rebuter le plus intrépide calculateur. J’ai, par exemple, consommé beaucoup de tems, et à diverses reprises, pour chercher l’enveloppe de l’espace parcouru par une corde de longueur constante qui roule dans une ellipse, sans jamais avoir pu conduire le calcul à sa fin; et pourtant, dans ce genre, on ne saurait guère se proposer de problèmes plus simples, du moins en apparence. La recherche des enveloppes intéresse particulièrement l’optique; puisque, dans cette science, c’est toujours aux caustiques qu’il en faut venir. Vous voyez donc, Monsieur, que vous rendriez un vrai service à la science si vous aviez quelque chose de nouveau à nous dire sur une matière aussi épineuse.
Vous avez dû être assez content, Monsieur, de la maniere dont M. Querret<1> a abordé le problème de votre série. C’est encore là une branche de l’analyse pour la quelle vous avez sans doute des recettes particulieres, si j’en juge du moins par les résultats curieux aux quels vous parvenez. J’accepte donc avec beaucoup de plaisir et de reconnaissance l’offre que vous voulez bien me faire d’un mémoire sur ce sujet.
Je n’ai point encore reçu, Monsieur, le mémoire de M. Babbage <2> que vous me faites l’honneur de m’annoncer. Lors qu’il me parviendra vous pouvez croire que je lui ferai tout l’accueil que mérite une production d’un géomètre aussi distingué.
Il y a deux mois que j’ai mis sur le chantier une Géométrie analytique, dont j’ai déja écrit 400 pages, quoi que je sois loin encore d’en être à la moitié. Vous voyez, Monsieur, que si l’ouvrage ne se recommande pas à d’autres tîtres, il se recommandera du moins par son poids et son volume. Excepté nos traités élementaires qui sont excessivement resserés, tout ce que nous avons sur cette branche de la science est disséminé dans beaucoup d’ouvrages de sorte qu’il est difficile de trouver sous sa main ce dont on peut avoir besoin. J’ai donc cru devoir céder aux sollicitations de quelques amis de Paris qui ont eu la bonté de penser que je pouvais faire sur cette matiere un ouvrage qui ne serait p[as]<3> dépourvu d’intérèt et d’utilité. Je tacherai de le terminer cet hiver et de le rendre le moins important qu’il se pourra.
Je desire, Monsieur, que votre voyage dans les plus belles contrées de l’Europe vous procure tout l’agrement que vous avez droit de vous en promettre, et vous prie d’agréer l’assurance de la plus sincère estime et considération de la part de votre tout dévoué
J D. Gergonne
A Monsieur
Monsieur W. H. Talbot,
Poste restante,
[illegible deletion] ou à Rome
Italie
Translation:
Montpellier
November 1st 1822
Sir
You shall receive shortly after this letter my October edition in which you will find several demonstrations of your elegant theorem on curves which touch all three sides of the same triangle.
Following your instructions, I have just made a little note to rectify the wording of the problem dealt with by Mr Sagani Michel (pag. 115) and to give the true solution. His equation
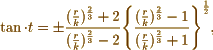
is indeed the equation of your curve, in which k is the semi-diameter of the hyperbola, or that which you took as your unit of measure. However I did not know exactly how this equation could be simplified to the very straightforward form
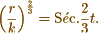
I seem to recall, Sir, having heard you say that you had a particular method, for investigating curve envelopes. This method must be far superior in order to give such results. It would be most precious to learn it; for although the problem of envelopes is very simple in theory, one encounters in its applications such eliminations as would put off even the most intrepid of calculators. I have, for example, spent a good deal of time, and on many occasions, trying to find the envelope of the space covered by a chord of constant length which rotates in an ellipse, without ever having been able to bring the calculation to its completion; and yet, of this type, it would be difficult to conceive of simpler problems, at least in appearance. Investigation of envelopes is of particular interest to the field of optics; since, in this science, it is always necessary to make use of caustics. You see therefore, Sir, that you will be doing a great service to science should you have anything new to tell us on such a thorny matter.
You must have been quite happy, Sir, with the manner in which Mr Querret approached the problem of your series. Here is another branch of analysis for which you must certainly have special formulae, at least if I am to judge by the curious results at which you arrive. I therefore accept with much pleasure and gratitude the offer which you were kind enough to put to me of a dissertation on the subject.
I have as yet not received, Sir, Mr Babbage’s thesis which you do me the honour of announcing. As soon as it reaches me you can be certain that I will give it the welcome which the production of such a distinguished geometrician merits.
I have been working for two months now on an Analytical Geometry, of which I have already written 400 pages, although I am still far from halfway through. You see, Sir, that if the work does not commend itself in other respects, it will commend itself at least by its weight and its volume. Apart from our elementary treatises which are excessively compressed, everything we have on this branch of science is spread through many works in such a way as to make it difficult to find that which we may require. I therefore thought I should yield to requests from friends in Paris who were so good as to think that I could produce on this subject a work which would not be lacking in interest and usefulness. I will try to finish it this winter and to make it the least imperfect possible.
I hope, Sir, that your journey through the most beautiful regions of Europe will procure you all the pleasure which you are entitled to hope of it, and I ask you to accept the assurance of the most sincere esteem and consideration from your ever devoted
J D. Gergonne
Mr. W. H. Talbot,
General Delivery,
[illegible deletion] Rome
Italy
Notes:
1. Jean Joseph Querret (1783-1839), Director of the Institute at St. Malo. See, for example, M. A. Legendre, translated by David Brewster, Elements of Geometry and Trignometry; with Notes (Edinburgh: Oliver & Boyd, 1822), p. v.
2. Text torn away under seal.
3. Prof Charles Babbage (1792–1871), mathematician & inventor.


