Lacock Abbey
25th Feb. 1835
Dear Sir
I have looked through Poisson’s paper in Crelle’s Journal <1> which I am obliged to you for pointing out <2> – I have no doubt that my method is more general – For instance suppose that X is a polynomial in x, as 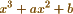 and that
and that 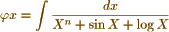 or any other assemblage of heterogeneous functions Then if φx + φy +φz = Const., let it be required to find the algebraic relation between x, y, z. I do not see that anything in Poission’s method can give any assistance in the solution of this & similar questions.
or any other assemblage of heterogeneous functions Then if φx + φy +φz = Const., let it be required to find the algebraic relation between x, y, z. I do not see that anything in Poission’s method can give any assistance in the solution of this & similar questions.
I hope to introduce into this subject a degree of simplicity which will permit it to be almost inserted in the Elements of the Integral Calculus. After establishing the Theory, the next thing will be to facilitate the practice of it. The great point is to be able to solve any proposed integral without having recourse to many transformations or other tentative methods. For that purpose order and classification will be necessary. In fact many of the results ought to be tabulated for reference, as in Hirsch’s Integral Tables <3>
In the example you have given of the solution of  from Abel’s theorem, <4> some of the roots are imaginary whenever n exceeds 4, which renders the solution illusory – It would be interesting to enquire whether the solution then becomes a real one with respect to some other integrals and if so, to exhibit the connection between them.
from Abel’s theorem, <4> some of the roots are imaginary whenever n exceeds 4, which renders the solution illusory – It would be interesting to enquire whether the solution then becomes a real one with respect to some other integrals and if so, to exhibit the connection between them.
Believe me
Dear Sir
Yours vy truly
H. F. Talbot
Notes:
1. Siméon Denis Poisson (1781–1840) mathematician, ‘Théorèmes relatifs aux intégrals des fonctions algébraiques’, Journal für die Reine und angewandte Mathematik, v.12 n.2, 1834 (article dated 1 December 1833) pp. 89–104.
2. See Doc. No: 03056.
3. Meyer Hirsch, (1765–1851) mathematician, Integral Tables or a Collection of Integral Formulae (London: William Banes & Son, 1823).
4. Written by Niels Henrik Abel (1802–1829), mathematician in 1824, lost in Paris and then rediscovered in 1828, this theorem proved the impossibility of solving equations of the fifth degree (quintic equations) through the use of radicals.


