My dear Sir,
The Letter <1> you did me the favor to write I transmitted to Mr Peacock. <2> I never doubted that your result was correct, & therefore I see no use in pushing your numerical example to more places of figures.
Pray refer to Legendre’s 2nd Supplement <3> p 163 & to his 3rd Supplement, also to a recent paper by Poisson <4> in Crelle’s Journal vol XII. p. 101. Mr Peacock & myself both think it indispensable that you should notice Abel’s Theorem, <5> which has created a revolution in this branch of mathematics.
It is very desirable moreover that the constant should be determined if possible.
In your first example & employing the notation of Legendre 2nd Supplement p 163 I find
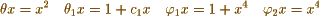
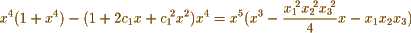
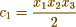
Now making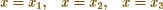 
successively
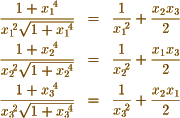
which are your equations.
Pray let me hear from you when you have compared the method of Abel with your own.
If you wish to have Legendre’s Supplements out of the Library of the Royal Society I will get them out for you & send them you by coach.
I am, dear Sir, Yours very truly,
J W Lubbock
29 Eaton Place <6>
27 Novr 1834
Notes:
1. See Doc. No: 03011.
2. Prof George Peacock (1791–1858), mathematician.
3. Adrien Marie Legendre (1752–1833), Traité des Fonctions Elliptiques et des Intégrals Eulériennes avec des Tables pour en Faciliter le Calcul Numérique (Paris: Huzard-Courcier, 1825); supplements were printed in 1828.
4. Siméon Denis Poisson (1781–1840), ‘Théorèmes relatifs aux intégrals des fonctions algébraiques’, Journal für die Reine und Angewandte Mathematik, v. 12 no. 2, 1834 (article dated 1 December 1833), pp. 89–104.
5. Written in 1824, lost in Paris and then rediscovered in 1828, this theorem proved the impossibility of solving equations of the fifth degree (quintic equations) through the use of radicals.
6. London.