My dear Sir,
I hope you got my last. I have lately had more time to consider the application of Abelís theorem <1> to your question & some others, having been before very much taken up with other subjects.
Your have no doubt ere this seen that your theorem about the arms of a hyperbola is one of the simplest cases of Abelís.
But I write this to rectify in one particular what I stated before. It would seem that Abelís theorem applied to integrals of the form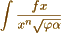
requires some little modification; at all counts, the integral
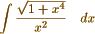
may be made to depend immediately upon

which is reached at once by Abelís theorem, & I arrive by this means at your result. So also for example
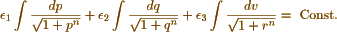
the equations of condition between, p, q & r bring those which you have employed. Ś1, Ś2, Ś3 being either +1 or −1. These integrals however of course in which the radical does not exceed four dimensions may be transformed into elliptic integrals by known methods.
I am, my dear Sir, Yours faithfully
J W Lubbock
18 Decr 1834
The Honble H F Talbot
Lacock Abbey
Chippenham
Notes:
1. Written in 1824, lost in Paris and re-written in 1828, this theorem proved the impossibility of solving equations of the fifth degree (quintic equations) through the use of radicals.


